Dynamic Programming

📝📓 record Dynamic Programming algorithm

Introduction

"Those who can not remember the past are condemned to repeat it", is often used to describe the Dynamic Programming, also called DP Algorithm. So, is repeating the things for which you already have the answer, a good thing? A programmer would disagree. That's what Dynamic Programming is about. To always remember answers to the sub-problems you've alreay solved.

We need to break up a problem into a series of overlapping sub-problems, and build up a solutions to larger and sub-probems. If you are given a problem, which can be broken down into smaller sub-problems, and these smaller sub-problems can be broken into smaller ones - and if you manage to find out that these are some overlapping subproblems, then you've encountered a DP problems.

In programming, Dynamic Programming is a powerful technique that allows one to solve different types of problems in time O(N^2) or O(N^3) for which a naive approach would take exponential time.

Following are the two main propertites of a problem that suggests that a given problem can be solved using DP

overlapping subproblem

optimal substructure

1. overlapping subproblem

In calculating fibonacci, we can see the function fib(3) is being called 2 times. if we would have stored the value of fib(3), then insted of computing it again, we could have reused the old stored value. There are following two different ways to store the value that these value can be reused:

Memoization (Top Down)
Tabulation (Bottom Up)

Memoization (Top Down)

The memoized program for a problem is similar to the recursive version with a small modification that it looks into a lookup table before computing solutions. We initilize a lookup table array with all initial values, whenever we need the solution to a subproblems, we first look into the lookup table, if the precomputed value is there then return that value, otherwise, we calculate the value and put the result in the lookup table so that it can be reused later. Following is the memoized version for Fibonacci Number:

int lookup_table[100];
for(int i = 0; i < 100; i ++)
	lookup_table[i] = -1;
int fibonacci(int n){
	if(lookup_table == -1){
		if(n <=1)
			lookup_table[n] = n;
		else
			lookup_table[n] = fibonacci(n - 1) + fibonacci(n - 2);
	}
	return lookup_table[n];

Tabulation (Bottom Up)

THe tabulated program for a given problem builds a table in bottom up fashion and returns the last entry from table. For example, for the same Fibonacci number, we first calculate fib(0) then fib(1) then fib(2) and so on. So iterally, we are building the solutions of subprolems bottom-up. Following is the tabulated version from Fibonacci Number:

int fibonacci(int n){
 	int a[n + 1];
	a[0] = 0;
	a[1] = 1;
	for(int i = 2; i <= n; i ++)
		a[i] = a[i - 1] + a[i - 2];
	return a[n];

2. optimal substructure

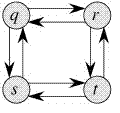
A given problem has optimal substructure propertity if optimal solution of the given problem can be obtained by using optimal solutions of it's subproblems. For example, the Shortest Path problem has following optimal substructure property: If a node x lies in the shortest path from a source node u to destination node v then the shortest path from u to v is combination of shortest path from u to x and shortest path from x to v. On the other hand, the Longest Path problem does'nt not have the. optimal substructure propertity, here, by longest path we mean longest simple path(path without cycle) between two nodes. there are two longest paths fromm q to t: q->s->t and q->r->t. Unlike shortest path, these longest path do not have the optimal substructure property. For example, the longest path q->r->t is not a combination of lonest path from q to r and longest path from r to t, because the longest path from q to r is q->s->t->r and the longest path from r to t is :r->q->s->t.

Dynamic Programming and Recursion

Dynamic Programming is basically, recursion plus using common sense. What it means that recursion allows you to repress the value of a function in terms of other values og that function. Where the common on sense tells you that if you implement your function in a way that the recursive calls are done in adavance, and stored for easy access, it will make your program faster. This is what we call Memoization — it is memoizating the results of some specific states, which can then be later accessed to solve other sub-problems.

The intuition behind dynamic programming is that we trade space for time. i.r. to say that insted of calculating all the states taking a lot of time but no space, we take up space to store the results of all the sub-problems to save time later.

Majority of the Dynamic Programming problems can be categorized into two types:

Optimization problems(最优值问题)
Combinatorial problems（组合优问题）

The optimization problems expect you to select a feasible solutions, so that the value of the required function is minimized or maximized. Combinatirial problems expect you to figure out the number of ways to do something, or the probability of some event happening.

The development of a dynamic programming algorith can be broken into a sequence of four steps.

Characterize the stracture of an optimal solution.
Recursively define the value of an optimal solution.
Compute an optimal solution from computed information.
Construct an optimal solution from computed information.

Step 1~3 form the basis of a dynamic programming solution to a problrms, step 4 can be omitted id only the value of an optimal solution is required. When we do perform step 4, we sometimes maintain additional information during the computation in step 3 to ease the construction of an optimal solution.

blog